У даній публікації розглянуто використання генетичного алгоритму для рішення задач оптимізації багатоекстремальних функцій і функцій з нелінійною не випуклою областю обмежень.
Отримані результати показали, що застосування генетичного алгоритму не може гарантувати знаходження найкращого рішення, проте, він з великою ймовірністю дає одне з оптимальних рішень.
Для покращення оптимізації необхідно робити детальний аналіз операторів кросенговера та мутації для генетичного алгоритму, адже збільшення розміру популяції чи кількості поколінь не завжди дають змогу отримати бажані результати.
Вступ
Еволюційні алгоритми (ЕА) є основою сучасних евристичних комп’ютерних технологій оптимізації, навчання, моделювання, проектування й управління у найширшому значенні цих понять. ЕА ґрунтуються на глибокій аналогії між біологічним генетичним кодом і комп’юте-рним двійковим кодом. Ця аналогія дає змогу формалізувати біологічний еволюційний процес і застосувати ідею про природний відбір для розв’язання найскладніших проблем у галузі природничих і комп’ютерних наук, промисловості та бізнесу [1-3].
У статті розглянуто один з таких методів – генетичні алгоритми (ГА). У їх основі лежить ідея використовувати аналоги еволюційних механізмів для пошуку рішення. Як відомо, основними концепціями теорії еволюції є спадковість і природний відбір [5]. Ці ж механізми використовуються генетичним алгоритмом для знаходження рішення.
Роботу ГА можна описати таким етапами. На самому початку випадковим чином ініціалізується популяція, яка має такі характеристики, як: чисельність, кількість генів у кожної особини і їх розрядність. Особини популяції оцінюються відповідно до вибраного критерію, і в результаті оцінки визначається їх пристосованість. Як критерій, виступає деяка функція F (g1, g2,…,gn), де gi – i-й ген особини, що оцінюється. Чим вище пристосованість особини, тим більша ймовірність того, що вона візьме участь в схрещуванні. При схрещуванні двох особин відбувається “обмін генетичною інформацією”, тобто відповідні гени обмінюються бітами. Дана операція називається кросенговером. Отримані в результаті схрещування нащадки формують нове покоління замість попереднього, і все повторюється спочатку, але вже для щойно створеного покоління. Алгоритм припиняє роботу в одному з наступних випадків:
- знайдено рішення;
- минув встановлений час роботи;
- популяція тривалий час не прогресує.
Після закінчення роботи найбільш пристосована особина популяції, точніше її гени, будуть представляти рішення задачі, знайдене ГА. Механізми, що закладені в основу ГА, не можуть гарантувати знаходження найкращого рішення, проте, вони з великою ймовірністю дають одне з оптимальних рішень.
Основною областю використання ГА є оптимізація багатоекстремальних функцій [4, 6-7, 9].
Постановка задачі оптимізації
Для того щоб коректно поставити задачу оптимізації, необхідно задати:
- Допустиму множину:
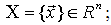
- Цільову функцію – відображення:
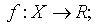
- Критерії пошуку (max чи min).
Тоді вирішити задачу ![]() означає одне із:
означає одне із:
- Показати, що X = Ø;
- Показати, що цільова функція
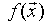 не обмежена знизу;
не обмежена знизу; - Знайти
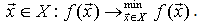
Існує чимало функцій для тестування роботи ГА, адже чим вони простіші – тим легше і швидше можна отримати бажаний результат. Більш складніші функції потребують спеціального аналізу операторів кросенговера та мутації для ГА. В багатьох випадках важливу роль також відіграє етап селекції кращих особин для подальшого схрещування.
Для демонстрації можливостей ГА взято складні функції, що мають значну популярність при аналізу ефективності роботи ГА [8, 10]:
- функція De Jong, або як її ще називають – «сферична модель». Вона безперервна і випукла (рис. 1).Визначення функції (1):
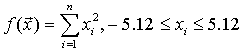
Глобальний мінімум f(x)=0, x(i)=0, i=1:n.
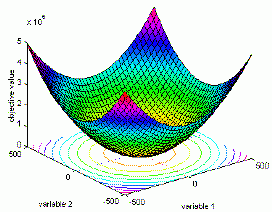
Рис. 1. Графічне зображення «сферичної моделі»
- «долина Розенброка» (функція De Jong 2) є класичною проблемою оптимізації. Глобальний оптимум знаходиться всередині повздовжньої, вузької, параболічної форми плоскої долини. Знайти «долину» не так складно, однак наблизитися до глобального оптимуму важко. Тому, ця проблема неодноразово використовується в оцінці діяльності алгоритмів оптимізації (рис. 2).Визначення функції (2):
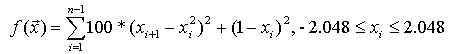
Глобальний мінімум f(x)=0; x(i)=1, i=1:n
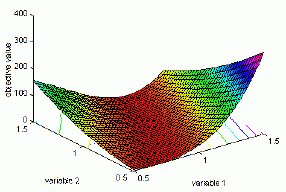
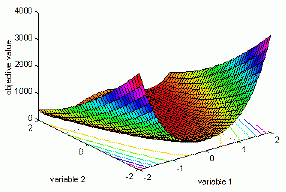
Рис. 2. Графічне зображення “долини Розенброка”
- функція Растрігіна. Вона грунтується на функції (1) з додаванням косинусної модуляції для створення багатьох локальних мінімумів. Таким чином, ця тестова функція є мультимодальною, а положення мінімумів розподілені регулярно (рис. 3).Визначення функції(3):
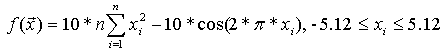
Глобальний мінімум f(x)=0; x(i)=0, i=1:n
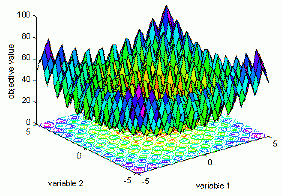
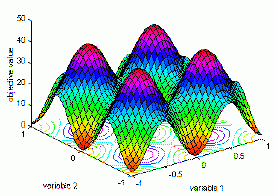
Рис. 3. Графічне зображення функції Растрігіна
Задача кодувалась таким чином, щоб її вирішення могло бути представлено в вигляді масиву подібного до інформації складу хромосоми.
Випадковим чином в масиві створювалась деяка кількість початкових елементів «осіб», або початкова популяція. Особи оцінювалися з використанням функції пристосування (фітнес-функція), в результаті якої кожній особі присвоювалось певне значення пристосованості, яке визначало можливість виживання особи. Після цього з використанням отриманих значень пристосованості вибирались особи допущені до схрещення (селекція).
До осіб застосовувалися “генетичні оператори” (оператор схрещення (crossover) і оператор мутації (mutation), що створювали таким чином наступне покоління осіб. Особи наступного покоління також оцінювалися застосуванням генетичних операторів і виконувалась селекція і мутація. Так моделювався еволюційний процес, що продовжувався декілька життєвих циклів (поколінь), поки не було виконано критерій зупинки алгоритму. Таким критерієм було:
- знаходження глобального, або надоптимального вирішення;
- вичерпання числа поколінь, що задані на еволюцію;
- вичерпання часу, заданого на еволюцію.
Границя пошуку складала 0,001. Тобто, якщо знайдений екстремум відрізнявся менш ніж на 0,001, то таку різницю не бралось до уваги.
Вимірність задач для кожної з функцій (1-3) залежала від 10-ти змінних. Популяція із 25-ти особин налічувала 250 змінних.
Фітнес-функції мали такий вигляд для задач (1-3):
- f(x)=sum(x(i)^2), i=1:n, -5.12<=x(i)<=5.12;
- f(x)=sum(100·(x(i+1)-x(i)^2)^2+(1-x(i))^2), i=1:n-1, -2.048<=x(i)<=2.048;
- f(x)=10·n+sum(x(i)^2-10·cos(2·pi·x(i))), i=1:n, -5.12<=x(i)<=5.12.
Для генетичного алгоритму було розроблено одно-точковий кросинговер (рис. 4). Коефіцієнт мутації (pm) був рівним 0,5 бітова мутація). Тип відбору – турнірний.
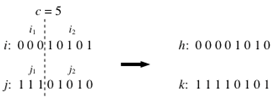
Рис. 4. Приклад одноточкового кросинговера
На рис. 4 показано приклад роботи одноточкового оператора кросинговеру. i,j – початкові батьківські хромосоми; h,k – новостворені особи, що містять гени від обох батьків в точці розриву c=5.
Для оптимізації багатоекстремальних функцій використовував ГА з однаковими параметрами, що наведені у табл.1. Також слід зауважити, що при оптимізації кожної функції було виконано 50 запусків ГА.
Таблиця 1. Характеристики ГА
| Розмір популяції | Макс. число поколінь | Розрядність генів |
| 25 | 100 | 10 |
Результати отримані при оптимізації функції (1) наведені у табл. 2. Fmin(x) – мінімальне значення фітнес-функції, яке було отримано в процесі оптимізації; Fmax(x) – максимальне значення фітнес-функції, яке було отримано в процесі оптимізації; N – число випадків коли було знайдено глобальний мінімум, а в дужках приведений процент від загальної кількості запусків.
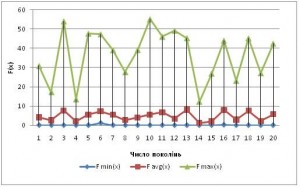
Також було проведено моніторинг фітнес-значень (результат F(x) цільової функції). Результати зображені на рис. 5. Fmin(x) – мінімальне фітнес-значення функції, що спостерігалось в процесі оптимізації серед всієї популяції; Fmax(x) – максимальне фітнес-значення функції, що спостерігалось в процесі оптимізації серед всієї популяції; Favg(x) – середнє фітнес-значення функції, що спостерігалось в процесі оптимізації серед всієї популяції.
Рис. 5. Моніторинг фітнес-значень при 20-ти запусках для функції (1)
Результати отримані при оптимізації функції (2) наведені у табл. 3. Позначення співпадають з табл. 2.
Таблиця 2. Результати оптимізації функції 1)
| Fmin(x) | Fmax(x) | N |
| 0 | 1,12 | 38 (76%) |
Таблиця 3. Результати оптимізації функції 2)
| Fmin(x) | Fmax(x) | N |
| 7,88 | 266,89 | 0 (0%) |
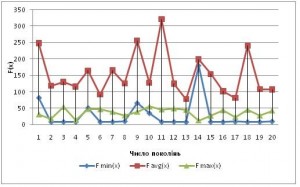
Моніторинг фітнес-значень зображено на рис. 6. Позначення такі ж самі, як і для рис. 5.
Рис. 6. Моніторинг фітнес-значень при 20-ти запусках для функції (2)
Із табл. 3 ми бачимо, що віднайти глобальний мінімум для функції Розенброка так і не вдалось. Локальний мінімум – 7,88. Це зумовлено складністю даної задачі.
Перейдемо до отриманих результатів при оптимізації функції (3) що наведені у табл. 4. Позначення співпадають з табл. 2-3.
Таблиця 4. Результати оптимізації функції 3)
| Fmin(x) | Fmax(x) | N |
| 0 | 0,06 | 48 (96%) |
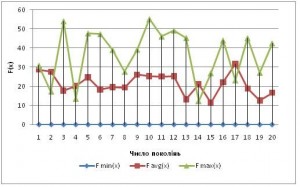
Моніторинг фітнес-значень для функції (3) зображено на рис. 7. Позначення такі ж самі як і для рис. 5-6.
Рис. 7. Моніторинг фітнес-значень при 20-ти запусках для функції (3)
Результати роботи ГА показали його придатність для оптимізації багатоекстремальних функцій. Для функцій (1) та (3) було знайдено глобальний мінімум при 76% та 96% відповідно. А ось для функції (2) «Долина Розенброка», глобального мінімум не було знайдено. Хоча до самої «долини» 7,88 було наближено, але досягти глобального оптимуму так і не вдалося. Це все зумовлено складністю цієї функції. Тому, вона неодноразово використовується в оцінці діяльності алгоритмів оптимізації.
Якщо Favg(x)>Fmax(x), то це свідчить про те, що популяція не прогресує, а навпаки – деградує. В такому випадку алгоритм зупиняє свою роботу. Це чітко видно на рис. 6.
Висновки
Ідея використання ГА для оптимізації багато екстремальних функцій досить цікава. Слід також відзначити, що для роботи ГА не потребуються громіздкі обрахунки.
Із отриманих значень в процесі тестування також слід відзначити, що глобальний екстремум у більшості випадків був отриманий при еволюціонуванні 50-60-го покоління.
Отримані результати показали, що кожна постановка задачі для ГА потребує унікального і специфічного підходу для розробки оператора кросенговера та мутації.
Інколи при вирішенні складних задач допомагає збільшення кількості генерацій для популяцій. Але з цим треба бути обережними та дозволяти алгоритму еволюціонувати тільки в тому випадку, якщо Favg(x)®min (при знаходженні глобального мінімуму).
Список літератури
- Жуков І.А., Кравець І.М. Розподілення навантаження баз даних в інформаційно-аналітичній системі // Проблеми інформатизації та управління: Зб. наук. пр. – К.: НАУ, 2007. Вип. 4(22). – С.56–61.
- Zhukov I.A., Kravets I.M. “Organization of distribution load database in the analysis and information system”, International scientific technical conference “DESSERT-2009”, Radioelectronic and computer system. Kharkiv, KhAI, 2009. – Vol. 5(39). – P. 25–30.
- Zhukov I.A., Kravets I.M. “An algorithm of fragmentation optimization in distributed database”, Advanced computer systems and networks design and application: proceedings of the 4-th International conference ACSN-2009. – Lviv, 2009. – P. 72–75.
- Rosenbrock, H.H. “An Automatic Method for Finding the Greatest or Least Value of a Function.”, Computer J. 3, 1960. – P. 175–184.
- Darrell Whitley. “A genetic algorithm tutorial” // Statistics and Computing. – Springer Netherlands. Vol. 4(2) / June, 1994. – PP. 65-85.
- Sharapov R., Lapshin A. “Convergence of genetic algorithms” // Pattern Recognition and Image Analysis. – MAIK Nauka/Interperiodica distributed exclusively by Springer Science+Business Media LLC. – Vol. 16(3) / July, 2006. – PP. 392-397
- Bäck, T. “Evolutionary Algorithms in Theory and Practice” // Evolution Strategies, Evolutionary Programming, Genetic Algorithms. – New York, Oxford: Oxford University Press, 1996.
- Pohlheim H. “Advanced Techniques for the Visualization of Evolutionary Algorithms”. Proceedings of 42. International Scientific Colloquium Ilmenau, 1997. – Vol. 3. – PP. 60–68.
- F. Herrera, M. Lozano, A.M. Sánchez. “Hybrid crossover operators for real-coded genetic algorithms: an experimental study” // Soft Computing – A Fusion of Foundations, Methodologies and Applications. – Springer Berlin / Heidelberg. – Vol. 9(4) / April, 2005. – PP. 280-298.
- Pohlheim H. GEATbx: Genetic and Evolutionary Algorithm Toolbox for use with Matlab. www.geatbx.com, 1994-2010.
УДК 004.658.3(045)
Оптимізація багатоекстремальних функцій за допомогою генетичного алгоритму / Кравець І.М.
Розглянуто використання генетичного алгоритму для рішення задач оптимізації багатоекстремальих функцій і функцій з нелінійною не випуклою областю обмежень. Отримані результати показали, що застосування генетичного алгоритму не може гарантувати знаходження найкращого рішення, проте, він з великою ймовірністю дає одне з оптимальних рішень. Для покращення оптимізації необхідно робити детальний аналіз операторів кросенговера та мутації для генетичного алгоритму, адже збільшення розміру популяції чи кількості поколінь не завжди дають змогу отримати бажані результати.
УДК 004.658.3(045)
Оптимизация многоэкстремальных функций с помощью генетического алгоритма / Кравец И.М.
Рассмотрено использование генетического алгоритма для решения задач оптимизации багатоекстремальных функций и функций с нелинейной не выпуклой областью ограничений. Полученные результаты показали, что применение генетического алгоритма не гарантирует нахождение наилучшего решения, однако, он с большой вероятностью дает одно из оптимальных решений. Для улучшения оптимизации необходимо делать детальный анализ операторов кросенговера и мутации для генетического алгоритма, ведь увеличение размера популяции или количества поколений не всегда позволяют получить желаемые результаты.
УДК 004.658.3(045)
Optimization of multi-extrema functions using genetic algorithm / Kravets I.M.
Usage of genetic algorithm for solving optimization problems of functions with multiple extrema, and functions with non-linear not convex range restrictions. Results has shown that using genetic algorithm cannot guarantee finding the best solution though it gives one of optimal solutions with high probability. To improve optimization, it is necessary to perform detailed analysis of crossover and mutation operators for genetic algorithm, as increasing of population or generation numbers does not always provide desired results.